
Régime linéaire - Circuits dépendants de la fréquence

L'étude est ici faite en régime harmonique en considérant les impédances complexes des différents composants. La boucle de contre-réaction induit un fonctionnement linéaire de l'amplificateur opérationnel (V+ = V-). Cette page ne décrit pas une étude complète et rigoureuse d'un filtre (pas de diagramme de Bode), mais se contente de proposer un montage dont le comportement est celui recherché (filtre passe-bas, passe-haut, passe-bande, ...). Il est supposé que le lecteur possède des notions sur le gain, les fréquences de coupure ainsi que sur le coefficient d'amortissement et de qualité d'un filtre.
Nommée cellule de Sallen & Key, cette structure est utilisée pour réaliser des filtres actifs du second ordre. On se propose ici d'en étudier le fonctionnement dans le cas général où chaque composant externe est représenté par son admittance complexe (inverse de l'impédance). La cellule de Sallen & Key met en oeuvre une double contre-réaction : positive et négative.
Pour débuter l'étude de ce montage, déterminons tout d'abord l'expression de la tension V1 grâce au théorème de Millman :
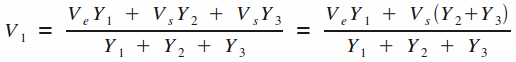
Ensuite, il est possible de connaitre l'expression de V2 en appliquant la formule du pont diviseur de tension entre les admittances Y3 et Y4 (attention, l'expression est légèrement différente de celle avec des impédances !) :
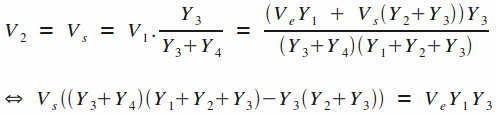
On en déduit ensuite facilement la relation entre l'entrée et la sortie qui caractérise la structure de Sallen & Key :
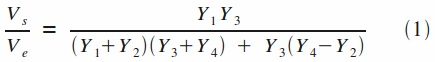
Pour ajouter un gain variable et positif au montage, il suffit d'ajouter un pont diviseur dans la boucle de contre-réaction négative. On parle alors de cellule de Sallen & Key à gain variable :

Exprimons tout d'abord la tension V2 en fonction de Vs par le biais d'un pont diviseur de tension (rappel : V+ = V-) :
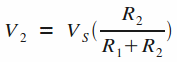
De la même manière que précédemment, on trouve :

Ce qui nous donne la relation suivante entre Vs et Ve :
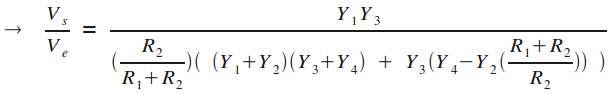
A des fins de simplification de cette expression, on peut poser :
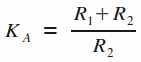
Au final, nous obtenons l'expression générale caractéristique d'une cellule de Sallen & Key à gain variable :
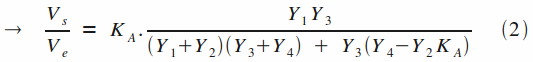
NB : Vous aurez peut être remarqué que l'ajout des résistances R1 et R2 forment avec l'AOP un amplificateur non-inverseur. On pourrait alors être tenté de simplement ajouter le gain KA à l'expression de la cellule simple, or il n'en n'est rien. En effet, la boucle de réaction influe sur le fonctionnement du montage et nous ne sommes plus en présence d'un simple amplificateur non-inverseur. L'expression finale ci-dessus met bien en avant que le gain KA se retrouve aussi au dénominateur. Attention donc aux raccourcis trop simplistes !
Les formules (1) et (2) permettent de calculer la réponse fréquentielle des montages du deuxième ordre suivants :