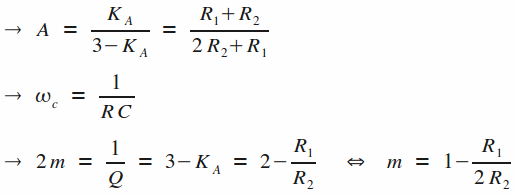Régime linéaire - Circuits dépendants de la fréquence

L'étude est ici faite en régime harmonique en considérant les impédances complexes des différents composants. La boucle de contre-réaction induit un fonctionnement linéaire de l'amplificateur opérationnel (V+ = V-). Cette page ne décrit pas une étude complète et rigoureuse d'un filtre (pas de diagramme de Bode), mais se contente de proposer un montage dont le comportement est celui recherché (filtre passe-bas, passe-haut, passe-bande, ...). Il est supposé que le lecteur possède des notions sur le gain, les fréquences de coupure ainsi que sur le coefficient d'amortissement et de qualité d'un filtre.
Ce montage utilise la structure de Sallen & Key légèrement modifiée pour produire un filtrage passe-bande. En effet, il faut ici noter la présence de la capacité C1 entre le point V1 et la masse. De fait, nous n'utiliserons pas la formule générale de la structure de Sallen & Key comme point de départ de nos calculs.
Tout d'abord fixons nous un objectif afin de savoir où nous allons dans nos calculs : obtenir une expression sous la forme normalisée d'un filtre passe-bande, telle que celle présentée ci-dessous :

Pour commencer les calculs, exprimons tout d'abord la tension V1 grâce au théorème de Millman :
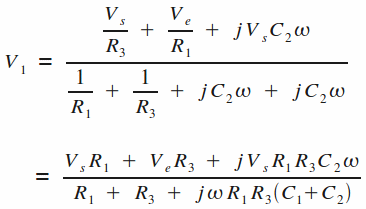
Pour obtenir la tensions V2, il suffit d'appliquer un pont diviseur (Vs = V2 ici, l'AOP étant monté en suiveur) :

En ramenant les termes en Vs à gauche de l'équation, il vient après simplification :
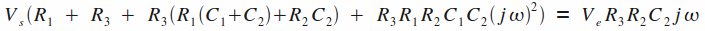
Il suit logiquement :
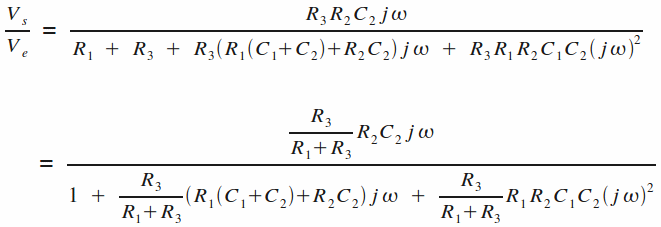
Afin de simplifier cette dernière expression, choisissons R1 = R2 = R et C1 = C2 = C pour obtenir :
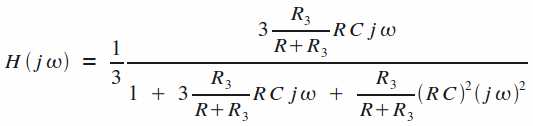
Ce qui nous permet d'identifier les différentes parties de la forme canonique :
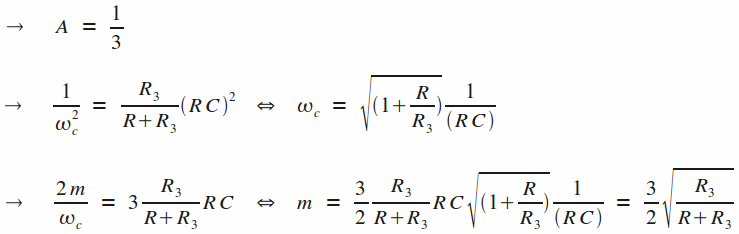
Pour changer le gain de ce montage, il est possible d'ajouter un pont diviseur dans la boucle de contre-réaction négative, on parle alors de cellule de Sallen & Key à gain variable (condensateurs et résistances sont fixés respectivement à C et R uniquement par soucis de simplification des expressions) :

A nouveau, nous n'allons pas utiliser de formule générale pour étudier ce montage. Exprimons la tension V1 grâce au théorème de Millman :
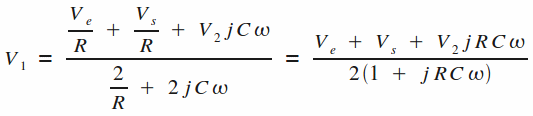
A l'instar du premier montage, la tension V2 s'obtient par le biais d'un pont diviseur de tension :
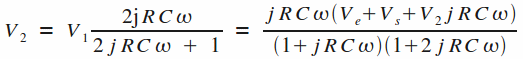
L'expression de la tension de l'entrée inverseuse (entrée "-") de l'AOP est obtenue via un pont diviseur à partir de Vs.
En appliquant maintenant l'équalité entre les deux tensions d'entrée de l'AOP (car présence d'une boucle de contre-réaction), il vient :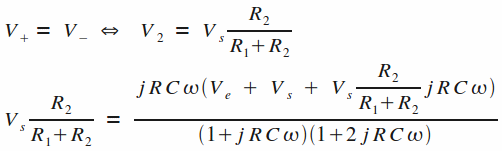
Ce que nous pouvons encore écrire en passant les termes en Vs à gauche de l'égalité et en posant le terme KA :
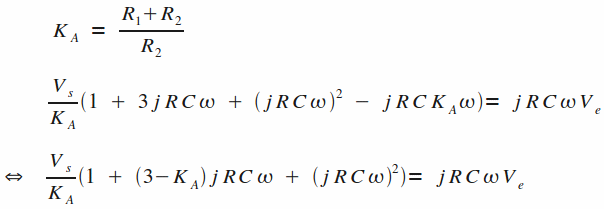
On en déduit donc la fonction de transfert H(jw) de ce montage (rapport Vs/Ve) :

Que l'on peut encore écrire pour coller avec la forme canonique d'un filtre passe-bande :

Cette dernière expression nous permet l'identification des termes génériques suivants :