
Régime linéaire - Circuits dépendants de la fréquence

L'étude est ici faite en régime harmonique en considérant les impédances complexes des différents composants. La boucle de contre-réaction induit un fonctionnement linéaire de l'amplificateur opérationnel (V+ = V-). Cette page ne décrit pas une étude complète et rigoureuse d'un filtre (pas de diagramme de Bode), mais se contente de proposer un montage dont le comportement est celui recherché (filtre passe-bas, passe-haut, passe-bande, ...). Il est supposé que le lecteur possède des notions sur le gain, les fréquences de coupure ainsi que sur le coefficient d'amortissement et de qualité d'un filtre.
Considérons tout d'abord l'impédance globale Z, résultat de la mise en parallèle de C et de R2 :
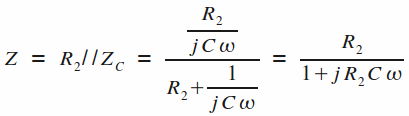
Ensuite, il suffit de reconnaitre que la structure et identique à un montage amplificateur inverseur pour déterminer la fonction de transfert H(jw) :

Nous obtenons la fonction de transfert caractéristique d'un filtre passe-bas du 1er ordre, elle-même multipliée par un gain fixé par les valeurs R2 et R (si R2 = R, on retrouve simplement l'opposé de la fonction de transfert d'une cellule R-C passe-bas). Il vous reste maintenant à étudier l'évolution du module et de la phase de H en fonction de la fréquence afin de tracer son diagramme de Bode.
NB : Attention, en pratique la bande passante de l'AOP est limitée !
Physiquement, l'impédance du condensateur diminuant avec la fréquence, plus celle-ci augmente, plus la boucle de contre-réaction se rapproche d'un simple fil (court-circuit de R2). De fait, malgré le gain R2/R, puisque l'AOP fonctionne en régime linéaire, on obtient V+ = V- = 0 V et donc la sortie se rapproche aussi de 0 V ! On "court-circuite" ainsi les hautes fréquences. Le comportement global du montage s'apparente donc bien à celui d'un filtre passe-bas.
NB : On reconnait ici la structure utilisée pour intégrer une tension continue (intégrateur).