L'amplificateur inverseur à gain renforcé

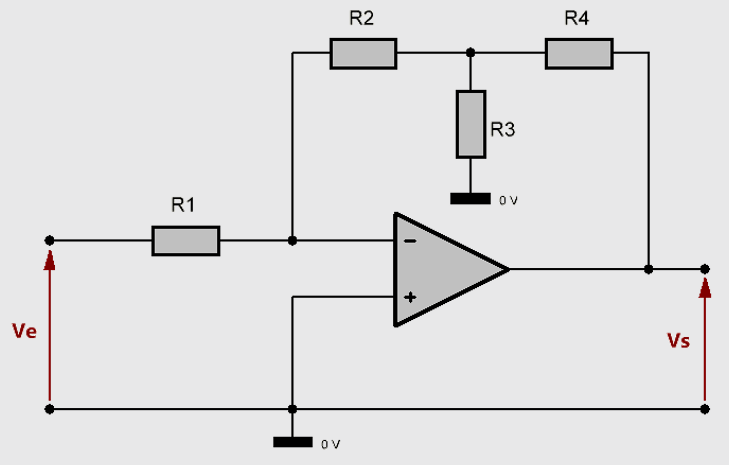$$\large V_s = -\frac{R_2}{R_1}\left(1 + R_4 \left(\frac{1}{R_2} + \frac{1}{R_3}\right) \right) V_e$$

L'AOP est supposé idéal et en régime linéaire, c'est-à-dire que $i_+ = i_- = 0$ et $V_+=V_-$ .

---

On considère les conventions suivantes pour les tensions et les courants :

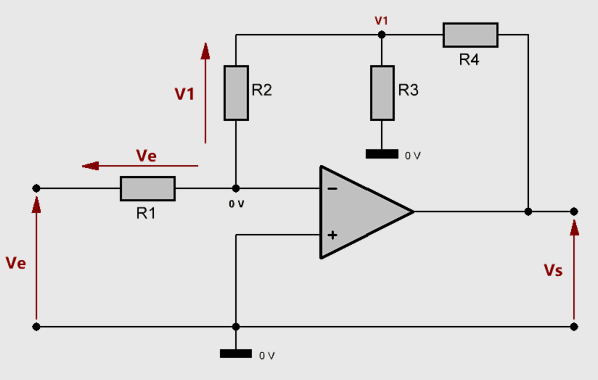
On commence par exprimer la tension $V_1$ aux bornes de $R_2$ sachant que cette dernière est à la masse puisque $V_+=V_-= 0 \, V$ .

Pour cela, on remarque que $V_1$ est la tension aux bornes de $R_2$ et $R_3$ en parallèle, ensemble nommé $R_{23}$ sur le schéma ci-dessous :

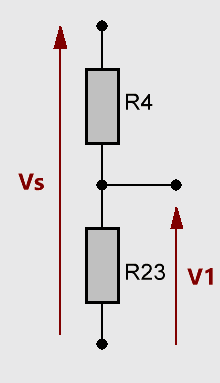
La formule du pont diviseur de tensions donne :

$$V_1= V_s \frac{R_{23}}{R_{23}+R_4}$$

Or (résitances en parallèles) :

$$ R_{23}=\frac{R_2R_3}{R_2+R_3}$$

donc il vient :

$$\begin{align*} V_1 & = V_s \frac{\frac{R_2R_3}{R_2+R_3}}{\frac{R_2R_3}{R_2+R_3}+R_4} \\ & = V_s \frac{R_2R_3}{R_2R_3 +R_4(R_2+R_3)} \end{align*}$$

Maintenant appliquons le théorème de Millman afin d'obtenir la tension de l'entrée inverseuse $V_-$ :

$$ \begin{align*} V_-& = \frac{\frac{V_e}{R_1} + \frac{V_1}{R_2}}{\frac{1}{R_1} + \frac{1}{R_2}} \\ & = \frac{\frac{V_eR_2}{R_1R_2} + \frac{V_1R_1}{R_1R_2}}{\frac{R_1+R_2}{R_1R_2}} \\ & = \frac{V_eR_2+V_1R_1}{R_1+R_2} \end{align*}$$

En remplaçant maintenant $V_1$ par l'expression calculée précedemment, on obtient :

$$V_- = \frac{V_eR_2+V_s\frac{R_1R_2R_3}{R_2R_3 +R_4(R_2+R_3)}}{R_1+R_2}$$

Or $V_+=V_- = 0 \, V$ (régime linéaire), ce qui implique que le numérateur est nul :

$$V_eR_2+V_s\frac{R_1R_2R_3}{R_2R_3 +R_4(R_2+R_3)} =0$$

Ce qui s'écrit encore :

$$V_eR_2 = -V_s\frac{R_1R_2R_3}{R_2R_3 +R_4(R_2+R_3)}$$

Finalement, on trouve l'expression suivante pour $V_s$ en fonction de $V_e$ :

$$ \begin{align*} V_s & = - V_eR_2 \frac{R_2R_3 +R_4(R_2+R_3)}{R_1R_2R_3} \\ & = - V_e\frac{R_2}{R_1}\left(\frac{R_2R_3 +R_4(R_2+R_3)}{R_2R_3} \right) \\ & = - V_e\frac{R_2}{R_1}\left(1 + \frac{R_4(R_2+R_3)}{R_2R_3} \right) \\ & = - V_e\frac{R_2}{R_1}\left(1 + R_4 \left(\frac{1}{R_2} + \frac{1}{R_3}\right) \right) \end{align*}$$

On retrouve bien l'expression caractéristique d'un amplificateur inverseur, mais multipliée par un coefficient positif qui est fonction de $R_2$, $R_3$ et $R_4$.