L'amplificateur inverseur
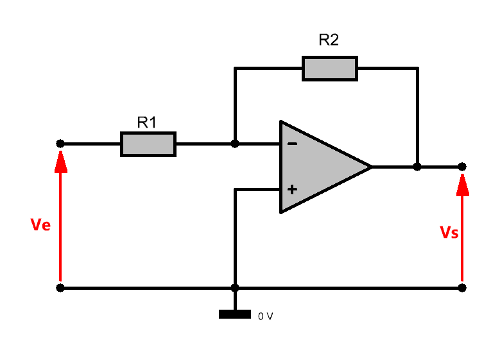$$\large V_s = -\frac{R_2}{R_1}V_e$$
On considère les conventions suivantes pour les tensions et les courants :
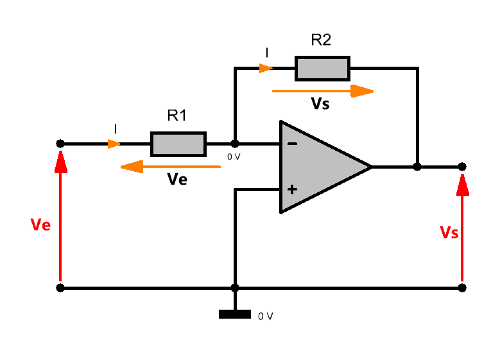
D'une part, le régime linéaire assure que $V_-= V_+ = 0 $. Ainsi, la tension $V_e$ se retrouve aux bornes de $R_1$ et $V_s$ aux bornes de $R_2$.
D'autre part, le courant circulant $I$ dans $R_1$ est le même que celui dans $R_2$ puisque $i_- = 0$. La loi d'Ohm appliquée à ces deux résistances donne :
$$I = \frac{V_e}{R_1} = -\frac{V_s}{R_2}$$L'égalité des produits en croix donne alors : $V_e \times R_2 = -V_s \times R_1$
Ce qui s'écrit également : $\frac{V_s}{V_e} = -\frac{R_2}{R_1}$
Soit, en multipliant chaque membre par $V_e$ : $$V_s = -\frac{R_2}{R_1} V_e$$
Le gain de ce montage est donnée par $-\frac{R_2}{R_1}$, il est donc négatif, de valeur absolue $\frac{R_2}{R_1}$.
La valeur absolue de la tension de sortie est donc supérieure à celle de la tension d'entrée si $\frac{R_2}{R_1} > 1$, inférieure si $\frac{R_2}{R_1} < 1$, ou égale si $\frac{R_2}{R_1} = 1$. Dans tous les cas, son signe est opposé à celui de $V_e$.
Le gain devenir réglable si l'on place des potentiomètres à la place de $R_1$ et/ou de $R_2$.