
Régime linéaire - Circuits dépendants de la fréquence

L'étude est ici faite en régime harmonique en considérant les impédances complexes des différents composants. La boucle de contre-réaction induit un fonctionnement linéaire de l'amplificateur opérationnel (V+ = V-). Cette page ne décrit pas une étude complète et rigoureuse d'un filtre (pas de diagramme de Bode), mais se contente de proposer un montage dont le comportement est celui recherché (filtre passe-bas, passe-haut, passe-bande, ...). Il est supposé que le lecteur possède des notions sur le gain, les fréquences de coupure ainsi que sur le coefficient d'amortissement et de qualité d'un filtre.
Ce montage utilise la structure de Rauch pour produire un filtrage passe-bas. Cette structure est caractérisée par la relation suivante :

Sachant qu'ici :
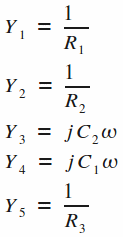
A savoir que nous cherchons à obtenir une fonction de transfert normalisée H de la forme passe-bande du second ordre:

Les calculs nous donnent, en remplacant dans l'équation générale chaque admittance par son expression :

En simplifiant le montage par un choix de capacités identiques, nous identifions les différents termes de la fonction de transfert :

La fonction de transfert obtenue correspond bien à celle d'un filtre passe-bande du deuxième ordre. Il vous reste maintenant à étudier l'évolution du module et de la phase de H en fonction de la fréquence afin de tracer le diagramme de Bode de ce montage.
Physiquement, les capacités C1 et C2 bloquent les signaux basses-fréquences au premier noeud. En hautes-fréquences, elles provoquent un court-circuit qui ramène la masse en sortie. Nous sommes donc bien en présence d'un filtre passe-bande.